Introduction
“Reflections on life and death of those who in Breslau lived and died” is the title of a manuscript that Protestant pastor Caspar Neumann sent to mathematician Gottfried Wilhelm Leibniz in the late 17th century. Neumann had spent years keeping track of births and deaths in his Polish hometown now called Wrocław. Unlike sprawling cities like London or Paris, Breslau had a rather small and stable population with limited migration in and out. The parishes in town took due record of the newly born and deceased.
Neumann’s goal was to find patterns in the occurrence of births and deaths. He thereby sought to dispel a persisting superstition that ascribed critical importance to certain climacteric years of age. Some believed it was age 63, others held it was either the 49th or the 81st year, that particularly critical events threatened to end the journey of life. Neumann recognized that his data defied the existence of such climacteric years.
Leibniz must have informed the Royal Society of Neumann’s work. In turn, the Society invited Neumann in 1691 to provide the Society with the data he had collected. It was through the Royal Society that British astronomer Edmund Halley became aware of Neumann’s work. A friend of Isaac Newton’s, Halley had spent years predicting the trajectories of celestial bodies, but not those of human lives.
After a few weeks of processing the raw data through smoothing and interpolation, it was in the Spring of 1693 that Halley arrived at what became known as Halley’s life table.
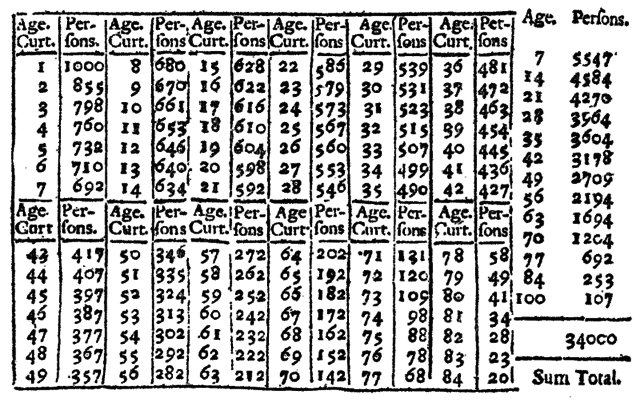
At the outset, Halley’s table displayed for each year of age, the number of people of that age alive in Breslau at the time. Halley estimated that a total of approximately 34000 people were alive, of which approximately 1000 were between the ages zero and one, 855 were between age one and two, and so forth.
Halley saw multiple applications of his table. One of them was to estimate the proportion of men in a population that could bear arms. To estimate this proportion he computed the number of people between age 18 and 56, and divided by two. The result suggested that 26% of the population were men neither too old nor too young to go to war.
At the same time, King William III of England needed to raise money for his country’s continued involvement in the Nine Years War raging from 1688 to 1697. In 1692, William turned to a financial innovation imported from Holland, the public sale of life annuities. A life annuity is a financial product that pays out a predetermined annual amount of money while the purchaser of the annuity is alive. The king had offered annuities at fourteen times the annual payout, a price too low for the young and too high for the old.
Halley recognized that his table could be used to estimate the odds that a person of a certain age would die within the next year. Based on this observation, he described a formula for pricing an annuity that, expressed in modern language, computes the sum of expected discounted payouts over the course of a person’s life starting from their current age.
Ambitions of the 20th century
Halley had stumbled upon the fact that prediction requires no physics. Unknown outcomes, be they future or unobserved, often follow patterns found in past observations. This empirical law would become the basis of consequential decision making for centuries to come.
On the heels of Halley and his contemporaries, the 18th century saw the steady growth of the life insurance industry. The industrial revolution fueled other forms of insurance sold to a population seeking safety in tumultuous times. Corporations and governments developed risk models of increasing complexity with varying degrees of rigor. Actuarial science and financial risk assessment became major fields of study built on the empirical law.
Modern statistics and decision theory emerged in the late 19th and early 20th century. Statisticians recognized that the scope of the empirical law extended far beyond insurance pricing, that it could be a method for both scientific discovery and decision making writ large.
Emboldened by advances in probability theory, statisticians modeled populations as probability distributions. Attention turned to what a scientist could say about a population by looking at a random draw from its probability distribution. From this perspective, it made sense to study how to decide between one of two plausible probability models for a population in light of available data. The resulting concepts, such as true positive and false positive, as well as the resulting technical repertoire, are in broad use today as the basis of hypothesis testing and binary classification.
As statistics flourished, two other developments around the middle of the 20th century turned out to be transformational. The works of Turing, Gödel, and von Neumann, alongside dramatic improvements in hardware, marked the beginning of the computing revolution. Computer science emerged as a scientific discipline. General purpose programmable computers promised a new era of automation with untold possibilities.
World War II spending fueled massive research and development programs on radar, electronics, and servomechanisms. Established in 1940, the United States National Defense Research Committee, included a division devoted to control systems. The division developed a broad range of control systems, including gun directors, target predictors, and radar-controlled devices. The agency also funded theoretical work by mathematician Norbert Wiener, including plans for an ambitious anti-aircraft missile system that used statistical methods for predicting the motion of enemy aircraft.
In 1948, Wiener released his influential book Cybernetics at the same time as Shannon released A Mathematical Theory of Communication. Both proposed theories of information and communication, but their goals were different. Wiener’s ambition was to create a new science, called cybernetics, that unified communications and control in one conceptual framework. Wiener believed that there was a close analogy between the human nervous system and digital computers. He argued that the principles of control, communication, and feedback could be a way not only to create mind-like machines, but to understand the interaction of machines and humans. Wiener even went so far as to posit that the dynamics of entire social systems and civilizations could be understood and steered through the organizing principles of cybernetics.
The zeitgeist that animated cybernetics also drove ambitions to create artificial neural networks, capable of carrying out basic cognitive tasks. Cognitive concepts such as learning and intelligence had entered research conversations about computing machines and with it came the quest for machines that learn from experience.
The 1940s were a decade of active research on artificial neural networks, often called connectionism. A 1943 paper by McCulloch and Pitts formalized artificial neurons and provided theoretical results about the universality of artificial neural networks as computing devices. A 1949 book by Donald Hebb pursued the central idea that neural networks might learn by constructing internal representations of concepts.
Pattern classification
Around the mid 1950s, it seemed that progress on connectionism had started to slow and would have perhaps tapered off had psychologist Frank Rosenblatt not made a striking discovery.
Rosenblatt had devised a machine for image classification. Equipped with 400 photosensors the machine could read an image composed of 20 by 20 pixels and sort it into one of two possible classes. Mathematically, the Perceptron computes a linear function of its input pixels. If the value of the linear function applied to the input image is positive, the Perceptron decides that its input belongs to class 1, otherwise class -1. What made the Perceptron so successful was the way it could learn from examples. Whenever it misclassified an image, it would adjust the coefficients of its linear function via a local correction.
Rosenblatt observed in experiments what would soon be a theorem. If a sequence of images could at all be perfectly classified by a linear function, the Perceptron would only make so many mistakes on the sequence before it correctly classified all images it encountered.
Rosenblatt developed the Perceptron in 1957 and continued to publish on the topic in the years that followed. The Perceptron project was funded by the US Office of Naval Research, who jointly announced the project with Rosenblatt in a press conference in 1958, that led to the New York Times to exclaim:
The Navy revealed the embryo of an electronic computer that it expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.“NEW NAVY DEVICE LEARNS BY DOING; Psychologist Shows Embryo of Computer Designed to Read and Grow Wiser,” The New York Times, 1958.
This development sparked significant interest in perceptrons and reinvigorated neural networks research throughout the 1960s. By all accounts, the research in the decade that followed Rosenblatt’s work had essentially all the ingredients of what is now called machine learning, specifically, supervised learning.
Practitioners experimented with a range of different features and model architectures, moving from linear functions to Perceptrons with multiple layers, the equivalent of today’s deep neural networks. A range of variations to the optimization method and different ways of propagating errors came and went.
Theory followed closely behind. Not long after the invention came a theorem, called mistake bound, that gave an upper bound on the number of mistakes the Perceptron would make in the worst case on any sequence of labeled data points that can be fit perfectly with a linear separator.
Today, we recognize the Perceptron as an instance of the stochastic gradient method applied to a suitable objective function. The stochastic gradient method remains the optimization workhorse of modern machine learning applications.
Shortly after the well-known mistake bound came a lesser known theorem. The result showed that when the Perceptron succeeded in fitting training data, it would also succeed in classifying unseen examples correctly provided that these were drawn from the same distribution as the training data. We call this generalization: Finding rules consistent with available data that apply to instances we have yet to encounter.
By the late 1960s, these ideas from perceptrons had solidified into a broader subject called pattern recognition that knew most of the concepts we consider core to machine learning today. In 1939, Wald formalized the basic problem of classification as one of optimal decision making when the data is generated by a known probabilistic model. Researchers soon realized that pattern classification could be achieved using data alone to guide prediction methods such as perceptrons, nearest neighbor classifiers, or density estimators. The connections with mathematical optimization including gradient descent and linear programming also took shape during the 1960s.
Pattern classification—today more popularly known as supervised learning—built on statistical tradition in how it formalized the idea of generalization. We assume observations come from a fixed data generating process, such as, samples drawn from a fixed distribution. In a first optimization step, called training, we fit a model to a set of data points labeled by class membership. In a second step, called testing, we judge the model by how well it performs on newly generated data from the very same process.
This notion of generalization as performance on fresh data can seem mundane. After all, it simply requires the classifier to do, in a sense, more of the same. We require consistent success on the same data generating process as encountered during training. Yet the seemingly simple question of what theory underwrites the generalization ability of a model has occupied the machine learning research community for decades.
Pattern classification, once again
Machine learning as a field, however, is not a straightforward evolution of the pattern recognition of the 1960s, at least not culturally and not historically.
After a decade of perceptrons research, a group of influential researchers, including McCarthy, Minsky, Newell, and Simon put forward a research program by the name of artificial intelligence. The goal was to create human-like intelligence in a machine. Although the goal itself was in many ways not far from the ambitions of connectionists, the group around McCarthy fancied entirely different formal techniques. Rejecting the numerical pattern fitting of the connectionist era, the proponents of this new discipline saw the future in symbolic and logical manipulation of knowledge represented in formal languages.
Artificial intelligence became the dominant academic discipline to deal with cognitive capacities of machines within the computer science community. Pattern recognition and neural networks research continued, albeit largely outside artificial intelligence. Indeed, journals on pattern recognition flourished during the 1970s.
During this time, artificial intelligence research led to a revolution in expert systems, logic and rule based models that had significant industrial impact. Expert systems were hard coded and left little room for adapting to new information. AI researchers interested in such adaptation and improvement—learning, if you will—formed their own subcommunity, beginning in 1981 with the first International Workshop on Machine Learning. The early work from this community reflects the logic-based research that dominated artificial intelligence at the time; the papers read as if of a different field than what we now recognize as machine learning research. It was not until the late 1980s that machine learning began to look more like pattern recognition, once again.
Personal computers had made their way from research labs into home offices across wealthy nations. Internet access, if slow, made email a popular form of communication among researchers. File transfer over the internet allowed researchers to share code and datasets more easily.
Machine learning researchers recognized that in order for the discipline to thrive it needed a way to more rigorously evaluate progress on concrete tasks. Whereas in the 1950s it had seemed miraculous enough if training errors decreased over time on any non-trivial task, it was clear now that machine learning needed better benchmarks.
In the late 1980s, the first widely used benchmarks emerged. Then graduate student David Aha created the UCI machine learning repository that made several datasets widely available via FTP. Aiming to better quantify the performance of AI systems, the Defense Advanced Research Projects Agency (DARPA) funded a research program on speech recognition that led to the creation of the influential TIMIT speech recognition benchmark.
These benchmarks had the data split into two parts, one called training data, one called testing data. This split elicits the promise that the learning algorithm must only access the training data when it fits the model. The testing data is reserved for evaluating the trained model. The research community can then rank learning algorithms by how well the trained models perform on the testing data.
Splitting data into training and testing sets was an old practice, but the idea of reusing such datasets as benchmarks was novel and transformed machine learning. The dataset-as-benchmark paradigm caught on and became core to applied machine learning research for decades to come. Indeed, machine learning benchmarks were at the center of the most recent wave of progress on deep learning. Chief among them was ImageNet, a large repository of images, labeled by nouns of objects displayed in the images. A subset of roughly 1 million images belonging to 1000 different object classes was the basis of the ImageNet Large Scale Visual Recognition Challenge. Organized from 2010 until 2017, the competition became a striking showcase for performance of deep learning methods for image classification.
Increases in computing power and volume of available data were a key driving factor for progress in the field. But machine learning benchmarks did more than to provide data. Benchmarks gave researchers a way to compare results, share ideas, and organize communities. They implicitly specified a problem description and a minimal interface contract for code. Benchmarks also became a means of knowledge transfer between industry and academia.
The most recent wave of machine learning as pattern classification was so successful, in fact, that it became the new artificial intelligence in the public narrative of popular media. The technology reached entirely new levels of commercial significance with companies competing fiercely over advances in the space.
This new artificial intelligence had done away with the symbolic reasoning of the McCarthy era. Instead, the central drivers of progress were widely regarded as growing datasets, increasing compute resources, and more benchmarks along with publicly available code to start from. Are those then the only ingredients needed to secure the sustained success of machine learning in the real world?
Prediction and action
Unknown outcomes often follow patterns found in past observations. But what do we do with the patterns we find and the predictions we make? Like Halley proposing his life table for annuity pricing, predictions only become useful when they are acted upon. But going from patterns and predictions to successful actions is a delicate task. How can we even anticipate the effect of a hypothetical action when our actions now influence the data we observe and value we accrue in the future?
One way to determine the effect of an action is experimentation: try it out and see what happens. But there’s a lot more we can do if we can model the situation more carefully. A model of the environment specifies how an action changes the state of the world, and how in turn this state results in a gain or loss of utility. We include some aspects of the environment explicitly as variables in our model. Others we declare exogenous and model as noise in our system.
The solution of how to take such models and turn them into plans of actions that maximize expected utility is a mathematical achievement of the 20th century. By and large, such problems can be solved by dynamic programming. Initially formulated by Bellman in 1954, dynamic programming poses optimization problems where at every time step, we observe data, take an action, and pay a cost. By chaining these together in time, elaborate plans can be made that remain optimal under considerable stochastic uncertainty. These ideas revolutionized aerospace in the 1960s, and are still deployed in infrastructure planning, supply chain management, and the landing of SpaceX rockets. Dynamic programming remains one of the most important algorithmic building blocks in the computer science toolkit.
Planning actions under uncertainty has also always been core to artificial intelligence research, though initial proposals for sequential decision making in AI were more inspired by neuroscience than operations research. In 1950-era AI, the main motivating concept was one of reinforcement learning, which posited that one should encourage taking actions that were successful in the past. This reinforcement strategy led to impressive game-playing algorithms like Samuel’s Checkers Agent circa 1959. Surprisingly, it wasn’t until the 1990s that researchers realized that reinforcement learning methods were approximation schemes for dynamic programming. Powered by this connection, a mix of researchers from AI and operations research applied neural nets and function approximation to simplify the approximate solution of dynamic programming problems. The subsequent 30 years have led to impressive advances in reinforcement learning and approximate dynamic programming techniques for playing games, such as Go, and in powering dexterous manipulation in robotic systems.
Central to the reinforcement learning paradigm is understanding how to balance learning about an environment and acting on it. This balance is a non-trivial problem even in the case where actions do not lead to a change in state. In the context of machine learning, experimentation in the form of taking an action and observing its effect often goes by the name exploration. Exploration reveals the payoff of an action, but it comes at the expense of not taking an action that we already knew had a decent payoff. Thus, there is an inherent tradeoff between exploration and exploitation of previous actions. Though in theory, the optimal balance can be computed by dynamic programming, it is more common to employ techniques from bandit optimization that are simple and effective strategies to balance exploration and exploitation.
Not limited to experimentation, causality is a comprehensive conceptual framework to reason about the effect of actions. Causal inference, in principle, allows us to estimate the effect of hypothetical actions from observational data. A growing technical repertoire of causal inference is taking various sciences by storm as witnessed in epidemiology, political science, policy, climate, and development economics.
There are good reasons that many see causality as a promising avenue for making machine learning methods more robust and reliable. Current state-of-the-art predictive models remain surprisingly fragile to changes in the data. Even small natural variations in a data-generating process can significantly deteriorate performance. There is hope that tools from causality could lead to machine learning methods that perform better under changing conditions.
However, causal inference is no panacea. There are no causal insights without making substantive judgments about the problem that are not verifiable from data alone. The reliance on hard earned substantive domain knowledge stands in contrast with the nature of recent advances in machine learning that largely did without—and that was the point.
Chapter notes
Halley’s life table has been studied and discussed extensively; for an entry point, see recent articles by BellhouseBellhouse, “A New Look at Halley’s Life Table,” Journal of the Royal Statistical Society: Series A (Statistics in Society) 174, no. 3 (2011): 823–32. and Ciecka,Ciecka, “Edmond Halley’s Life Table and Its Uses,” Journal of Legal Economics 15 (2008): 65–74. or the article by Pearson and Pearson.Pearson and Pearson, “The History of Statistics in the 17th and 18th Centuries Against the Changing Background of Intellectual, Scientific and Religious Thought,” British Journal for the Philosophy of Science 32, no. 2 (1981): 177–83.
Halley was not the first to create a life table. In fact, what Halley created is more accurately called a population table. Instead, John Grount deserves credit for the first life table in 1662 based on mortality records from London. Considered to be the founder of demography and an early epidemiologist, Grount’s work was in many ways more detailed than Halley’s fleeting engagement with Breslau’s population. However, to Grount’s disadvantage the mortality records released in London at the time did not include the age of the deceased, thus complicating the work significantly.
Mathematician de Moivre picked up Halley’s life table in 1725 and sharpened the mathematical rigor of Halley’s idea. A few years earlier, de Moivre had published the first textbook on probability theory called “The Doctrine of Chances: A Method of Calculating the Probability of Events in Play”. Although de Moivre lacked the notion of a probability distribution, his book introduced an expression resembling the normal distribution as an approximation to the Binomial distribution, what was in effect the first central limit theorem. The time of Halley coincides with the emergence of probability. Hacking’s book provides much additional context, particularly relevant are Chapter 12 and 13.Hacking, The Emergence of Probability: A Philosophical Study of Early Ideas about Probability, Induction and Statistical Inference (Cambridge University Press, 2006).
For the history of feedback, control, and computing before cybernetics, see the excellent text by Mindell.Mindell, Between Human and Machine: Feedback, Control, and Computing Before Cybernetics (JHU Press, 2002). For more on the cybernetics era itself, see the books by KlineKline, The Cybernetics Moment: Or Why We Call Our Age the Information Age (JHU Press, 2015). and Heims.Heims, The Cybernetics Group (MIT Press, 1991). See BenigerBeniger, The Control Revolution: Technological and Economic Origins of the Information Society (Harvard University Press, 1986). for how the concepts of control and communication and the technology from that era lead to the modern information society.
The prologue from the 1988 edition of Perceptrons by Minsky and Papert presents a helpful historical perspective. The recent 2017 reprint of the same book contains additional context and commentary in a foreword by Léon Bottou.
Much of the first International Workshop on Machine Learning was compiled in an edited volume, which summarizes the motivations and perspectives that seeded the field.Michalski, Carbonell, and Mitchell, eds., Machine Learning: An Artificial Intelligence Approach (Springer, 1983). Langley’s article provides helpful context on the state of evaluation in machine learning in the 1980s and how the desire for better metrics led to a renewed emphasis on pattern recognition.Langley, “The Changing Science of Machine Learning” (Springer, 2011). Similar calls for better evaluation motivated the speech transcription program at DARPA, leading to the TIMIT dataset, arguably the first machine learning benchmark dataset.Liberman, “Obituary: Fred Jelinek,” Computational Linguistics 36, no. 4 (2010): 595–99; Church, “Emerging Trends: A Tribute to Charles Wayne,” Natural Language Engineering 24, no. 1 (2018): 155–60; Liberman and Wayne, “Human Language Technology,” AI Magazine 41, no. 2 (2020): 22–35.
It is worth noting that the Parallel Distributed Processing Research Group led by Rummelhart and McLeland actively worked on neural networks during the 1980s and made extensive use of the rediscovered back-propagation algorithm, an efficient algorithm for computing partial derivatives of a circuit.McClelland, Rumelhart, and Group, “Parallel Distributed Processing,” Explorations in the Microstructure of Cognition 2 (1986): 216–71.
A recent article by Jordan provides an insightful perspective on how the field came about and what challenges it still faces.Jordan, “Artificial Intelligence—the Revolution Hasn’t Happened Yet,” Harvard Data Science Review 1, no. 1 (2019).